# Written assignments This page will show you the best way to complete and format written assignments in my courses. Suppose we are near the end of an algebra course, and this is the problem statement: |Assignment 12| |---| |Find the x-intercepts of the following function. <br> $f(x) = \dfrac{2x+1}{x+1} + \dfrac{3}{2x-4}$| ## Content |Evaluation|Work| |---|---| |**Incorrect:** Barely any work. Although it's a correct answer, I have no evidence that the problem was solved by you. Do your own work on written assignments. I grade on correct answer, correct steps, and clarity.|$f(x) = 0$ <br><br> $-\dfrac{1}{4}, 1$| |**Correct:** Correct answer, clear and correct steps. Sufficient balance of work and explanation. Not every step needs to be narrated. In this example, the steps involving simplifying and other algebraic arithmetic, the student already mastered earlier in the course.|To find the x-intercepts of $f(x)$, I am looking for all real numbers x that solve:<br><br> $\dfrac{2x+1}{x+1} + \dfrac{3}{2x-4} = 0$ <br><br> To ensure finding all solutions and no extraneous ones, I need to add the fractions. <br><br> $\dfrac{(2x+1)(2x-4)}{(x+1)(2x-4)} + \dfrac{3(x+1)}{(2x-4)(x+1)} = 0$ <br><br> $\dfrac{4x^2-6x-4}{2x^2-2x-4} + \dfrac{3x+3}{2x^2-2x-4} = 0$ <br><br> $\dfrac{4x^2-6x-4+3x+3}{2x^2-2x-4} = 0$ <br><br> $4x^2-3x-1 = 0$ <br><br> $(4x+1)(x-1) = 0$ <br><br> $x = -\dfrac{1}{4}, 1$ <br><br> Both these x-values are in the domain of $f(x)$, so they are not extraneous solutions. These are both x-intercepts of the graph of $f(x)$.| ## Format |Example|Description| |---|---| ||**Correct:** You can either write or type your assignments. The above solutions are examples of correct typesetting. You can use LaTeX or the equation editor of your word processor, or [online editors such as this one.](https://editor.codecogs.com/) If you remain in the sciences you will be well-served to learn the [LaTeX Markup Language](https://mathvault.ca/latex-guide/). If you write your solution, use pencil and paper so that you can fix small mistakes now and in future attempts. You can scan or photograph it.| |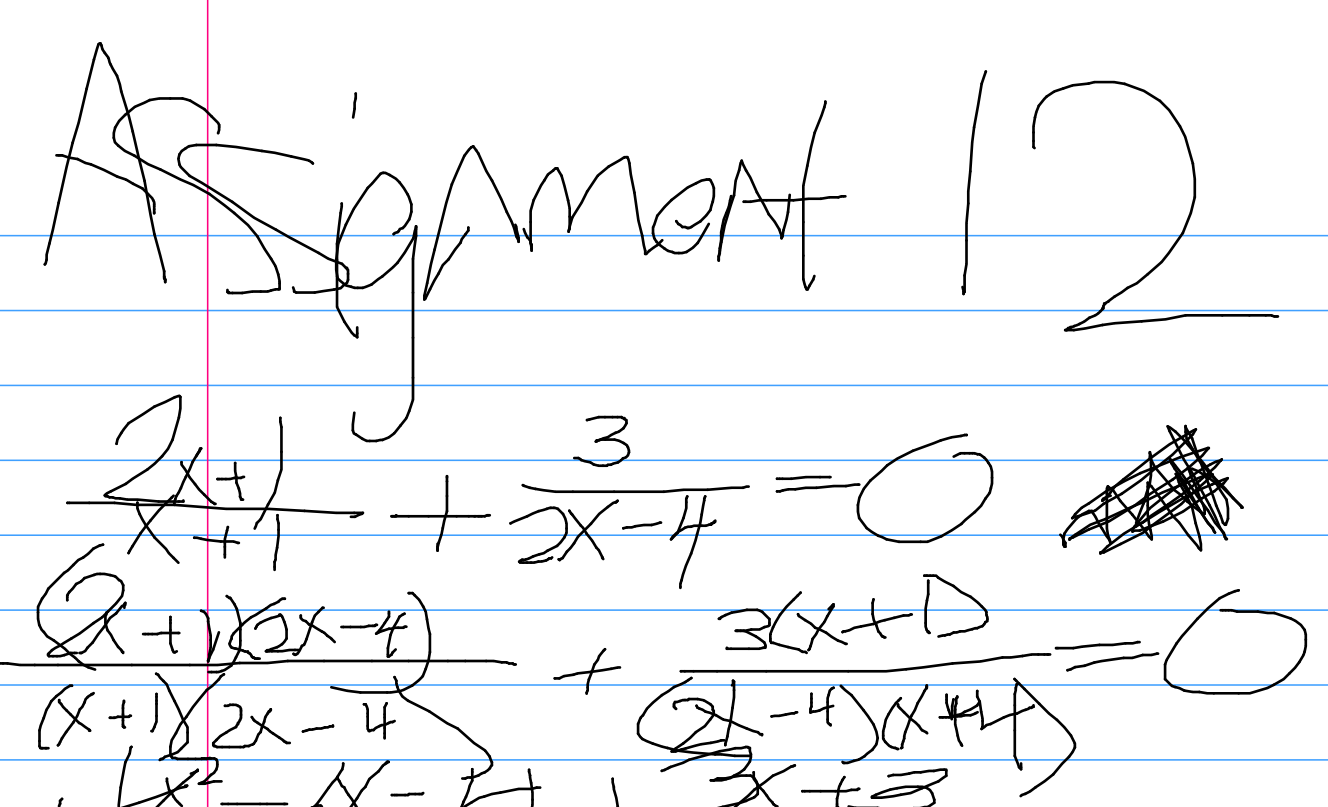|**Incorrect:** Messy, disorganized. We are in college, so write professionally.| ||**Incorrect:** Blurry, too dark/light, too low resolution, or otherwise unreadable.| |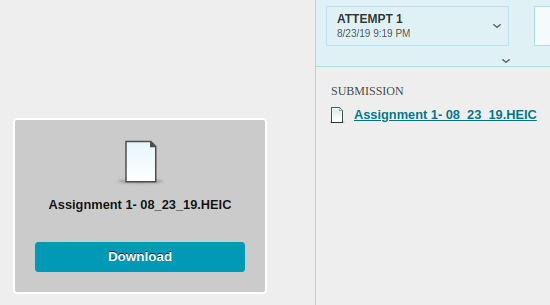|**Incorrect:** Not a recognized file type. Needs to be an image or document file stored locally on your device and uploaded directly to Blackboard. (Do not send me links to Google Drive, Imgur, Discord or other sites. Blackboard can host the images fine.) Working formats include: pdf, png, jpg, doc, docx. Always preview your uploaded assignment to confirm it shows up.| |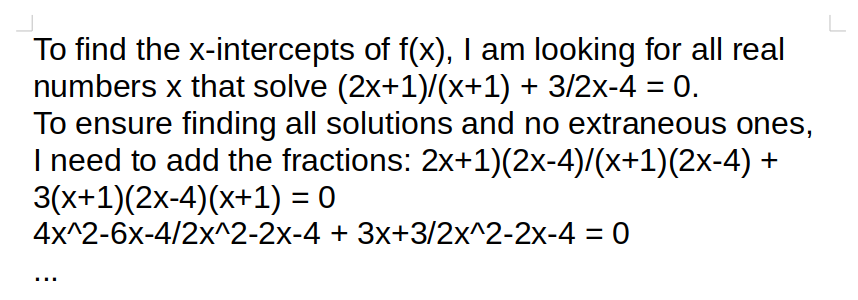|**Incorrect:** Typed but not equation-formatted. PLEASE do not do this! It's a migraine to interpret, and it's prone to ambiguity that can change the entire meaning of your equations.| **Incorrect** uploads will need to be reformatted and/or rewritten, and reuploaded. ## Upload process This was done on a desktop computer. Phones may behave differently or not at all. |Step|Picture| |---|---| | 1. On the blackboard course, open the Assignments folder. Find the assignment you are completing. Click "Start Attempt 1", then open the PDF to see the instructions. (You may need to download it.)|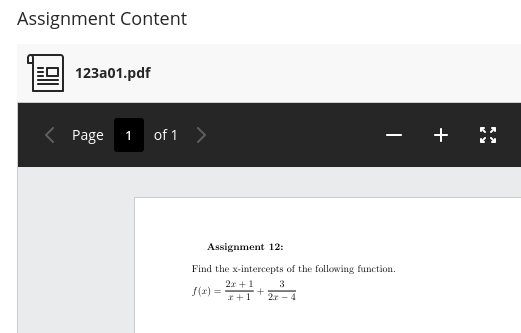| | 2. When you are ready to upload, drag and drop your file into the submission box. Confirm it looks okay and click Submit. It will warn that you can’t make changes, submit anyway. I allow as many re-attempts as needed. If you click “Save” or “Save draft” but not “Submit”, I will not be able to see or grade your assignment. If days pass and you haven’t gotten a grade, this is usually why. <br><br> If you catch a mistake or upload the wrong file, don't worry. Follow the submission instructions again. I will grade your most recent attempt.| <br> 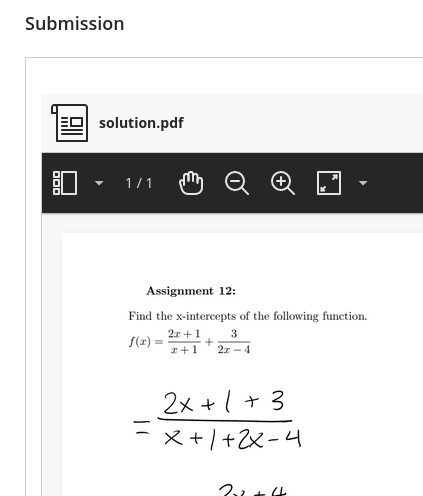| | 3. After the due date, to view your grade and feedback, open the assignment again and click on Attempt 1 (or the most recent).|| | 4. Feedback can be found directly on the document, or to the right. If you turned in an attempt on time but got a zero, read the feedback and make corrections, and reupload the assignment by following these steps again. (Click the "Start Attempt _" button). If there is a 0 and no feedback, something went wrong. Let me know if this happens and I will fix it.|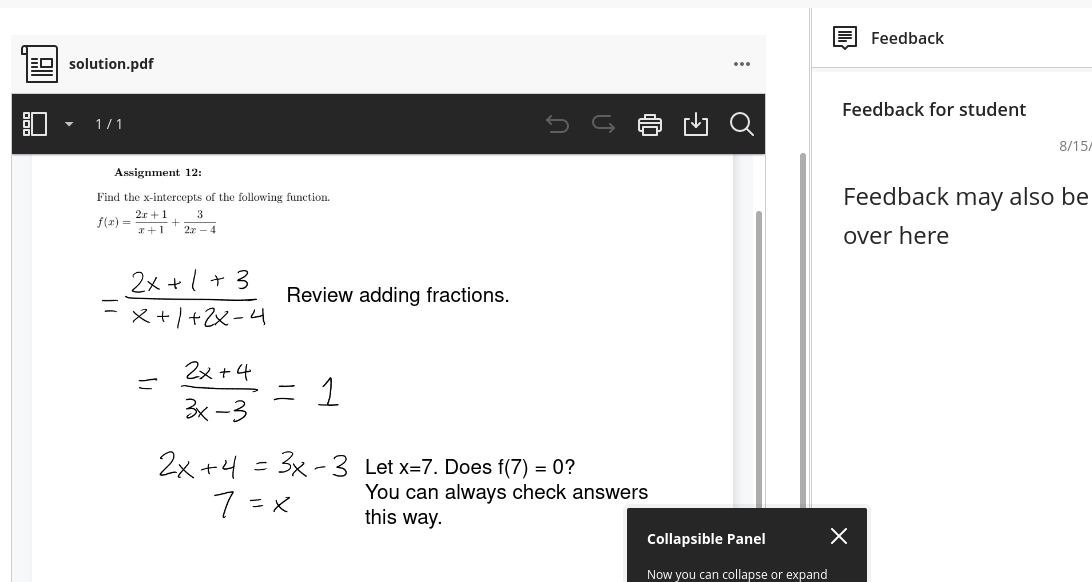| ## A note on AI Why do I require writing? An often overlooked aspect of mathematics is accurate communication. You are arguing a case. You are solving a problem. You are walking through your thought process with someone else in order to prove to them you are correct. But most importantly, you are proving to yourself and me that you know what you're doing. By this point, LLMs (Large language models) have made major strides. They can turn text prompts into "pictures" in seconds, carry on a "conversation", and write an "essay" -- including a math solution. But LLMs fundamentally operate by asking repeatedly "based on the last x words, which word is most likely to come next?" Any appearance of thought or logic that forms from this process is illusory. The main question you should ask about anything an LLM says is "How do I know that this is correct?" In all my courses, no electronics of any kind are allowed on written in-class tests. Whatever resources you use in the meantime, whether online tutorial videos, LLMs, or anything not yet invented, make sure it is serving your understanding and ability to do the objectives. I design assignments to be obstacle courses to test the objectives you have just learned about. If you cannot do the obstacle course yourself, you will not be ready for the test. There is no replacement for doing the work. LLMs and other tools would not exist without humans. They are nothing more than math. If you learn math, you will understand exactly how AI works and what its limitations are. With enough work, you will even be able to create your own models to assist you in specific goals.